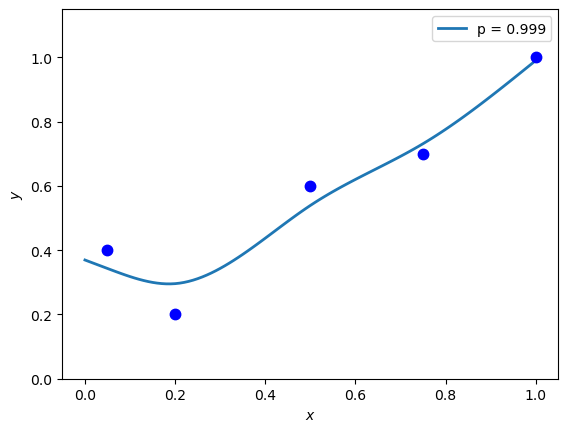
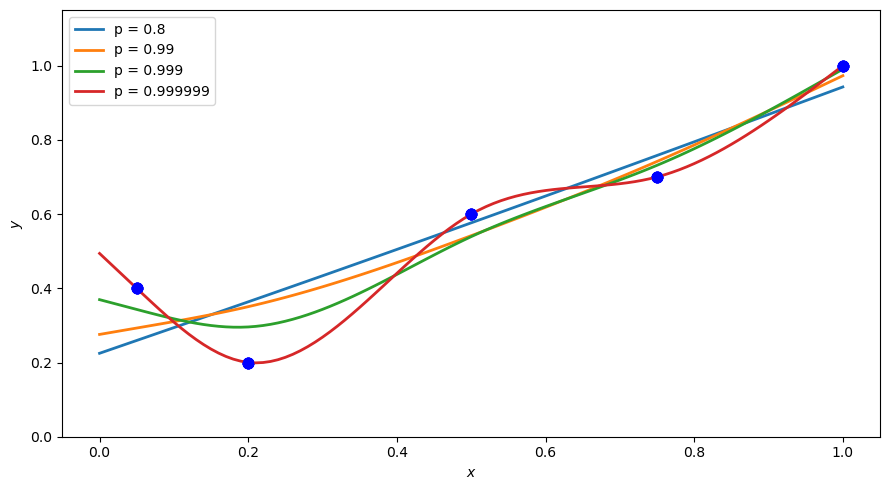
''' smoothspline_fig.py '''
# %%
import matplotlib.pyplot as plt
import numpy as np
#from matplotlib import rc
#rc('text', usetex=True)
x = np.array([[0.05, 0.2, 0.5, 0.75, 1.]]).T
y = np.array([[0.4, 0.2, 0.6, 0.7, 1.]]).T
n = x.shape[0]
plt.clf()
p_vals = [0.8, 0.99, 0.999, 0.999999]
plt_params = ['-', '-', '-', '-']
k = lambda x1, x2 : (1/2)* np.max((x1,x2)) * np.min((x1,x2)) ** 2 - \
((1/6)* np.min((x1,x2))**3)
for p, prm in zip(p_vals, plt_params):
ngamma = (1-p)/p
K = np.zeros((n,n))
for i in range(n):
for j in range(n):
K[i,j] = k(x[i], x[j])
Q = np.hstack((np.ones((n,1)), x))
m1 = np.hstack((K @ K.T + (ngamma * K), K @ Q))
m2 = np.hstack((Q.T @ K.T, Q.T @ Q))
M = np.vstack((m1,m2))
c = np.vstack((K, Q.T)) @ y
ad = np.linalg.solve(M,c)
# plot the curves
xx = np.arange(0,1+0.01,0.01).reshape(-1,1)
g = np.zeros_like(xx)
Qx = np.hstack((np.ones_like(xx), xx))
g = np.zeros_like(xx)
N = np.shape(xx)[0]
Kx = np.zeros((n,N))
for i in range(n):
for j in range(N):
Kx[i,j] = k(x[i], xx[j])
g = g + np.hstack((Kx.T, Qx)) @ ad
plt.plot(xx, g, prm, label = 'p = {}'.format(p), linewidth = 2)
plt.plot(x,y, 'b.', markersize=15)
plt.ylim((0,1.15))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.gcf().set_size_inches(9,5)
plt.tight_layout()
plt.legend()